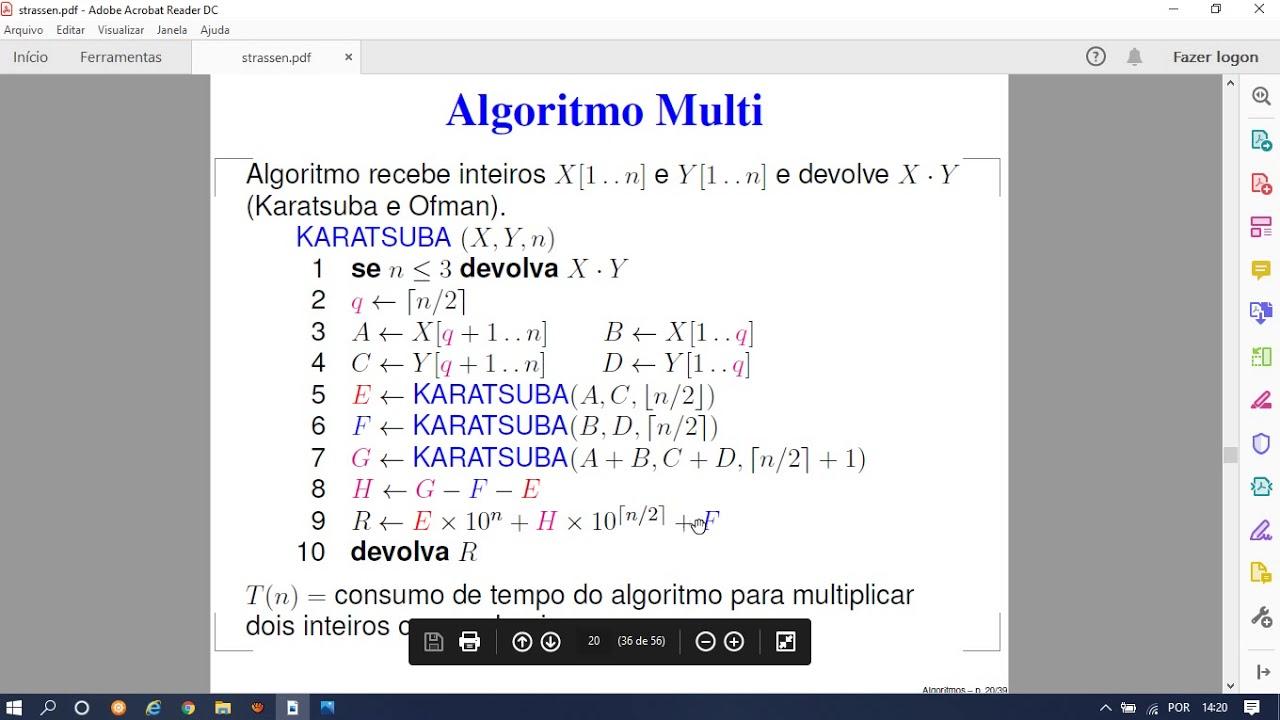
- Karatsuba reduce las multiplicaciones grandes de 4 a 3 mediante divide y vencerás, bajando la complejidad a Θ(n^{1,585}).
- El método se apoya en descomponer x e y en base B, combinar z2, z0 y (x1+x0)(y1+y0), y recomponer por potencias de B.
- Históricamente derribó la conjetura de Kolmogórov y abrió paso a Toom–Cook y Schönhage–Strassen hasta O(n·log n) en 2019.
Cuando multiplicamos números pequeños, tiramos de cabeza y sale casi sin pensar; con cifras grandes, la cosa cambia y solemos recurrir a papel, calculadora o a una librería de software. La multiplicación entera de gran tamaño no solo es una curiosidad: está en el corazón del cifrado, el álgebra computacional y muchos sistemas de cálculo.
En ese escenario aparece el algoritmo de Karatsuba, una idea brillante que reduce el número de multiplicaciones necesarias reemplazando algunas por sumas y desplazamientos. El truco divide y vencerás logra bajar la complejidad del método clásico, que es cuadrática, a una potencia menor, abriendo la puerta a multiplicaciones mucho más rápidas a gran escala.
Por qué importa multiplicar más rápido y los límites del método clásico
El método escolar tradicional (la multiplicación en columnas) es fácil de entender: multiplicamos cada dígito de un número por cada dígito del otro y sumamos los parciales alineados por posición. Con números de n dígitos por término, eso nos obliga a hacer en torno a n^2 productos elementales, además de muchas sumas.
De forma más formal, el procedimiento estándar requiere un número de operaciones proporcional a n^2, es decir, Θ(n^2) en notación asintótica. Si llamamos c1 al tiempo de cada multiplicación elemental y c2 al de cada suma, el tiempo medio puede aproximarse por c1·n^2 + c2·n^2. Como multiplicar suele costar más que sumar, para n grande se aproxima bien por c1·n^2.
Para ponerlo en números, pensemos en 4572 × 3169 con el método de toda la vida. Ambos tienen 4 dígitos, así que habrá 16 productos elementales y un número similar de sumas para acumular los parciales. Ese patrón de crecimiento cuadrático se vuelve pesadísimo según escalamos, y es justo el cuello de botella que los algoritmos rápidos tratan de aliviar.
Históricamente, se llegó a pensar que no había mucho margen de mejora. La intuición de “si hubiese algo mejor ya lo habríamos encontrado” caló durante décadas. Sin embargo, la historia dio un giro fulminante en un seminario de Moscú en 1960.
Historia: de la conjetura de Kolmogórov al hallazgo de Karatsuba
En los años 50, Andrey N. Kolmogórov intentó sostener que el algoritmo clásico era asintóticamente óptimo; en términos técnicos, que cualquier método para multiplicar necesitaba, en el peor caso, Ω(n^2) operaciones. En otoño de 1960 organizó un seminario sobre cibernética en la Universidad Estatal de Moscú donde compartió esa suposición y otros retos de complejidad computacional.
Solo una semana después, Anatoly Karatsuba, entonces un estudiante (según distintas fuentes, con 23 o 25 años), presentó un enfoque divide y vencerás que realizaba la multiplicación en Θ(n^{log_2 3}) operaciones, es decir, con exponente ≈ 1,585. Aquello derribó la conjetura de Kolmogórov y, según se cuenta, le dejó muy desilusionado; él mismo comunicó el resultado en la siguiente y última sesión del seminario.
El trabajo vería la luz en 1962 en Proceedings of the USSR Academy of Sciences. El artículo, presumiblemente redactado por el propio Kolmogórov (posiblemente con Yuri Ofman), nombraba como autores a A. Karatsuba y Yu. Ofman. Curiosamente, Karatsuba supo de la publicación cuando recibió un ejemplar de la revista; no había intervenido en el proceso editorial. A partir de 1963, ya traducido, se desató una cascada de avances en multiplicación y más allá.
La defensa original de Kolmogórov, muy influyente por su prestigio, había caído en una trampa lógica: un argumento ad ignorantiam. Que no existieran pruebas de un algoritmo mejor no implicaba que no pudiera existir. Karatsuba demostró lo contrario con una idea tan sencilla como poderosa.
El algoritmo de Karatsuba, explicado
La idea central es descomponer los operandos y recombinar de forma inteligente los productos parciales. Sea una base B (base posicional en la que escribimos los números) y tomemos dos n-dígitos x e y. Elegimos un entero m con 0 < m < n y partimos cada número en dos “mitades” de tamaño similar:
x = x1·B^m + x0 y y = y1·B^m + y0, con x0, y0 < B^m. Si desarrollamos el producto, obtenemos:
xy = (x1·B^m + x0)(y1·B^m + y0) = z2·B^{2m} + z1·B^m + z0, donde z2 = x1y1, z1 = x1y0 + x0y1, z0 = x0y0. El desarrollo directo utiliza 4 multiplicaciones “grandes”.
Karatsuba observó que z1 puede calcularse sin multiplicar dos veces cruzado. Basta con computar tres productos: z2 = x1y1, z0 = x0y0, y t = (x1+x0)(y1+y0). Entonces z1 = t − z2 − z0. Con ello, el costo pasa de 4 multiplicaciones a solo 3 multiplicaciones (más sumas y restas, que son más baratas), y recomponemos xy como antes.
Este paso básico funciona para cualquier base B y cualquier m, aunque el algoritmo recursivo rinde mejor cuando m ≈ n/2 (redondeando por exceso). Si n es una potencia de dos, y paramos la recursión cuando n=1, el número de productos de un dígito es 3^k si n=2^k, esto es n^c donde c = log2(3). Además, podemos “ampliar” con ceros a la izquierda hasta la siguiente potencia de dos, con lo que el número de multiplicaciones elementales cumple 3^{⌈log2 n⌉} ≤ 3·n^{log2 3}.
Hay pequeños atajos: si, por ejemplo, y1 = 0 (la mitad alta de y es cero), basta con dos productos ya que z2=0, z0=x0y0, z1=x1y0. Estos casos degenerados aparecen al final de la recursión y recortan aún más trabajo.
Una ventaja práctica importante es que las sumas, restas y desplazamientos por potencias de B son lineales en n; su peso relativo decrece según crece n. En notación de recurrencia, si t(n) es el coste total al multiplicar dos números de n dígitos, podemos escribir t(n) = 3·t(⌈n/2⌉) + c·n + d para constantes c y d. Aplicando el Teorema Maestro, se obtiene la cota asintótica t(n) = Θ(n^{log 3 / log 2}).
Complejidad, ejemplo detallado e implementación práctica
Veamos un ejemplo concreto con base 10 para que se vea la mecánica en acción. Tomemos x=1234 e y=5678, elegimos B=10 y m=2, con lo que 1234 = 12·10^2 + 34 y 5678 = 56·10^2 + 78. Calculamos los tres productos “grandes” de Karatsuba: z2 = 12×56 = 672, z0 = 34×78 = 2652, y t = (12+34)(56+78) = 46×134 = 6164. Entonces z1 = t − z2 − z0 = 6164 − 672 − 2652 = 2840.
Ya solo queda recomponer: xy = z2·B^{2m} + z1·B^m + z0 = 672·10^4 + 2840·10^2 + 2652 = 7.006.652. Con tres multiplicaciones principales, más sumas y desplazamientos decimales, llegamos al mismo resultado que el método clásico con cuatro multiplicaciones grandes.
El algoritmo se aplica recursivamente: cada uno de los productos z2, z0 y t puede calcularse, a su vez, con Karatsuba cuando los operandos siguen siendo grandes. La recursión se detiene cuando los números son lo suficientemente pequeños como para multiplicarlos de forma directa (método escolar o multiplicación nativa de la CPU).
Desde el punto de vista de la arquitectura, hay elecciones de base B muy convenientes. En una máquina con multiplicador ALU completo de 32×32 bits, escoger B=2^31=2.147.483.648 o B=10^9=1.000.000.000 permite almacenar cada “dígito” en una palabra de 32 bits. Con esas bases, sumas del tipo x1+x0 o y1+y0 no necesitan un dígito extra de acarreo (como en un carry-save adder), y podemos aplicar la recurrencia hasta el caso base de un “dígito”.
Conviene tener en mente que, para n pequeño, el recargo de sumas y movimientos puede hacer que Karatsuba sea más lento que el método en columnas. El punto de cruce depende de la plataforma y del contexto: caches, latencias, implementación concreta… Algunas fuentes sitúan la ventaja de Karatsuba para operandos enormes (del orden de 2^320 ≈ 2×10^96 o mayores), mientras que en la práctica de librerías modernas suele activarse mucho antes con tamaños moderados; en todo caso, siempre hay un umbral a partir del cual compensa.
Matemáticamente, el coste total satisface la recurrencia t(n) = 3·t(⌈n/2⌉) + c·n + d, cuya solución asintótica es Θ(n^{log 3 / log 2}) ≈ Θ(n^{1,585}). La mejora frente a Θ(n^2) no es marginal: al duplicar n, el trabajo crece por un factor ≈ 2^{1,585} en vez de 4. Y si necesitamos forzar que n sea potencia de dos, basta con completar con ceros a la izquierda; el número de multiplicaciones elementales queda acotado por 3^{⌈log2 n⌉} ≤ 3·n^{log2 3}.
Más allá de Karatsuba, el progreso no se detuvo. Toom y Cook (1966) generalizaron la idea y redujeron la cota, y en 1971 Schönhage y Strassen introdujeron un algoritmo basado en la Transformada Rápida de Fourier (FFT) para seguir empujando los límites. Estos autores además propusieron que el límite inferior plausible de la multiplicación fuera del orden n·log n.
Décadas después, en 2019, David Harvey y Joris van der Hoeven presentaron un método que alcanza O(n·log n) en tiempo, apoyándose también en FFT pero llevándola a 1729 dimensiones. Aunque la ganancia práctica frente a otros métodos cercanos no siempre es enorme y requiere tamaños descomunales para brillar, el logro teórico es rotundo: se ha llegado a la cota conjeturada.
Si te preguntas por qué no se enseña Karatsuba en Primaria, la respuesta es simple: para números pequeños el método clásico es óptimo en la práctica, y la sobrecarga de Karatsuba no compensa. En cambio, las librerías de enteros grandes en lenguajes de programación sí lo utilizan; de hecho, suelen implementar varios algoritmos (clásico, Karatsuba, Toom-Cook, FFT, etc.) y eligen dinámicamente el más adecuado según el tamaño. A medida que la recursión baja a operandos más pequeños, pueden incluso “cambiar de marcha” y rematar con la multiplicación estándar.
Para profundizar, hay fuentes de referencia muy valiosas: Knuth, The Art of Computer Programming, Vol. 2, artículos técnicos como el de Karatsuba–Ofman, compendios como MathWorld y notas de D. J. Bernstein sobre multiplicación multidígito, además de recursos prácticos (calculadoras en línea) que implementan Karatsuba y variantes.
Referencias y lecturas recomendadas
- Karacuba A. A. Berechnungen und die Kompliziertheit von Beziehungen. Elektron. Informationsverarb. Kybernetik 11, 603–606 (1975).
- Knuth D. E. The Art of Computer Programming, Vol. 2. Addison–Wesley (1969).
- MathWorld: Karatsuba Multiplication (en inglés)
- Bernstein, D. J. Multidigit multiplication for mathematicians. Revisión de Karatsuba y otros métodos.
- Multiplicación de Karatsuba en Fast Algorithms y la FEE; Karatsuba usando cuadrados de una diferencia; calculadoras en línea que lo implementan.
La moraleja que deja esta historia es doble: por un lado, una idea ingeniosa puede tumbar convicciones muy asentadas; por otro, la mejora de Θ(n^2) a Θ(n^{1,585}) basta para marcar una diferencia tangible en problemas reales con números gigantes. Con variantes modernas que llegan a O(n·log n) y sistemas que escogen el algoritmo idóneo según el tamaño, el paisaje actual de la multiplicación de enteros es más rico y eficiente que nunca.