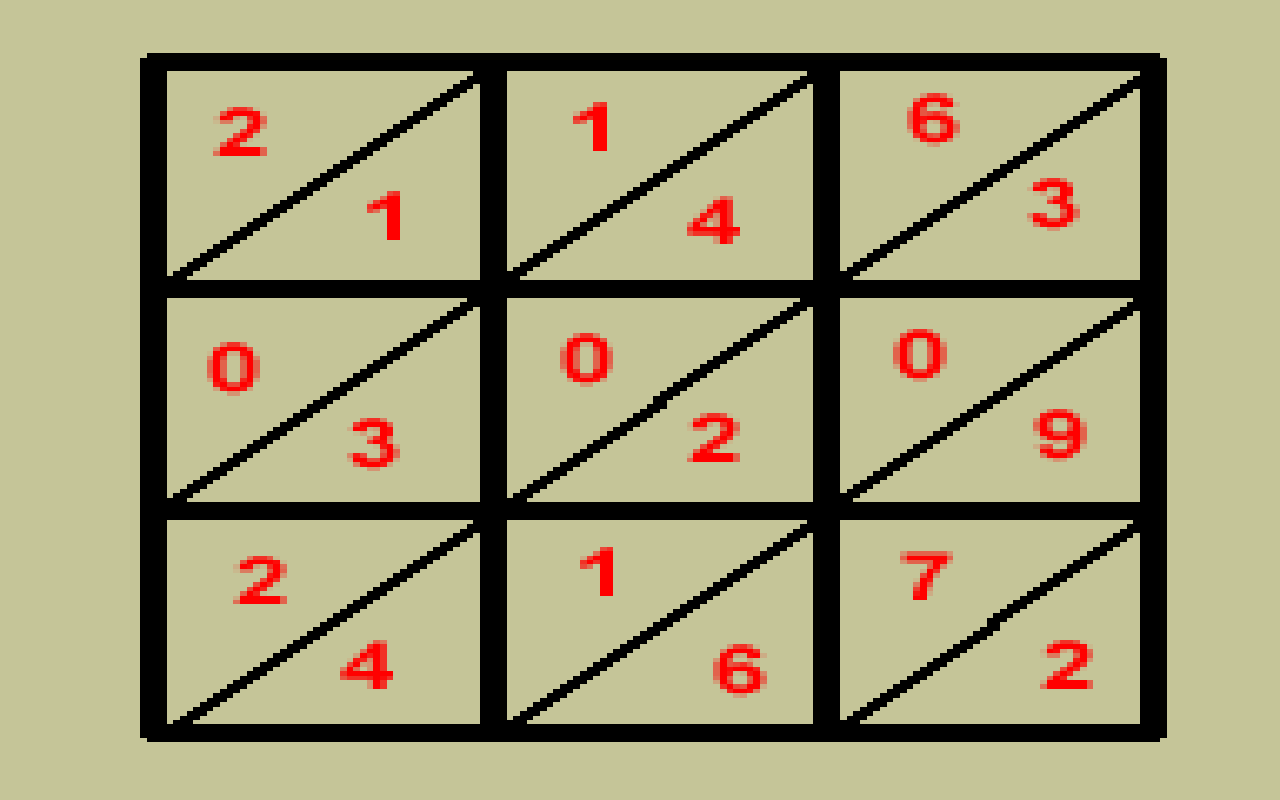
- Qué es la celosía: multiplicación visual con cuadrícula y diagonales.
- Origen renacentista (Pacioli) y encaje en 3.º-5.º de Primaria.
- Ventajas didácticas y resolución de errores comunes.
- Recursos en español, incluido un PDF breve y práctico.
Si buscas una forma visual y ordenada de multiplicar, el método de la celosía es una alternativa muy didáctica al algoritmo tradicional. En esta guía vas a encontrar una explicación clara, contextualizada históricamente y con ideas prácticas para aplicarlo en clase o en casa, incluyendo referencias a materiales en español que ya se usan en cursos de 3.º a 5.º. A lo largo del texto irás viendo cómo esta técnica encaja con enfoques modernos de enseñanza y por qué sigue vigente desde hace siglos, con un enfoque paso a paso y consejos para evitar errores comunes.
La idea central es sencilla: se dibuja una cuadrícula con diagonales, se multiplican dígitos por dígitos y se suman los resultados a lo largo de esas diagonales. Esto ayuda a ordenar la información y a reducir confusiones habituales con las llevadas. Y, aunque parezca novedosa, su historia se remonta al Renacimiento: el procedimiento fue atribuido al italiano Luca Pacioli en el siglo XV, lo que le otorga un encanto histórico además de su valor pedagógico. A partir de ahí, verás cómo se estructura, qué ventajas aporta y qué recursos en español puedes consultar (incluido un PDF breve y muy útil que ya ha acumulado centenares de visualizaciones entre docentes y familias).
¿Qué es el método de la celosía y cómo se organiza la cuadrícula?
El método de la celosía es una técnica de multiplicación por descomposición de cifras que traduce el proceso a un tablero con casillas. Se dibuja una rejilla con tantas columnas como cifras tenga el multiplicando y tantas filas como cifras tenga el multiplicador; cada casilla se divide por una diagonal. De este modo, cada multiplicación de dígitos ocupa un lugar concreto y el resultado de dos cifras se reparte: decenas en la parte superior izquierda, unidades abajo a la derecha. Gracias a esta estructura, la suma final se realiza recorriendo las diagonales, lo que facilita la gestión de las llevadas.
En términos prácticos, si multiplicas un número de tres cifras por otro de dos, tendrás tres columnas por dos filas. Cada intersección corresponde a un producto parcial (dígito por dígito). Cuando completes todas las casillas, sumarás los valores a lo largo de las diagonales inclinadas, de derecha a izquierda, arrastrando las llevadas a la diagonal siguiente cuando sea necesario. Esta presentación visual ayuda a entender de dónde viene cada cifra del resultado global y reduce el riesgo de saltarse pasos o mezclar columnas.
Una de las razones por las que este método gusta tanto en Primaria es que hace explícita la relación entre posición y valor. Las diagonales separan naturalmente unidades, decenas, centenas, etc., de forma que las alumnas y los alumnos ven con nitidez cómo se combinan los productos parciales. De hecho, para quienes se inician con multiplicaciones de dos o tres cifras, la celosía supone un puente entre el conteo y el cálculo posicional.
Además, el tablero admite personalización: se puede ampliar o reducir según el tamaño de los números, colorear diagonales para resaltar zonas de suma o incluso plastificar para reutilizar. Esta flexibilidad visual resulta muy útil para quienes aprenden mejor con apoyos gráficos y para docentes que desean progresar desde ejemplos sencillos hacia retos más complejos sin cambiar de método.
Un poco de historia y su encaje didáctico en Primaria
El procedimiento se popularizó en textos de aritmética del Renacimiento y es común atribuírselo a Luca Pacioli, figura clave del siglo XV. En aquellos manuales, la cuadrícula con diagonales se presentaba como una forma elegante de organizar los cálculos, especialmente útil para el comercio y el aprendizaje. Esta herencia histórica no es un simple dato curioso: pone de manifiesto que la estructura posicional y las sumas por diagonales llevan siglos funcionando para domar la complejidad de las multiplicaciones largas.
En el contexto actual, se emplea con frecuencia en los cursos intermedios de Primaria. Existe material en español pensado para 3.º a 5.º que sintetiza la técnica en unos pocos folios, con foco en ejercicios sencillos y ejemplos ilustrados. Un documento de referencia muy difundido es un PDF en español de tres páginas, alojado en una biblioteca pública, que sirve como hoja de habilidades o guía rápida; dicho material ha reunido en torno a mil visitas, lo cual sugiere que hay una demanda real por explicaciones claras y de rápida consulta.
Este encaje por edades se explica porque, entre los 8 y los 11 años, el alumnado ya reconoce el valor posicional de las cifras y puede multiplicar dígitos individuales, pero a veces se atasca con el algoritmo tradicional por disponer de muchas llevadas y cambios de fila. Al dividir el proceso en casillas y diagonales, se reduce la carga cognitiva y se ofrece un recorrido más lineal: primero productos parciales, después suma ordenada de diagonales hasta completar el resultado.
Por supuesto, el método no es excluyente: puede convivir con la multiplicación estándar. Muchas y muchos docentes lo introducen como recurso paralelo para reforzar comprensión, no como sustituto obligatorio. Ahí está su principal fortaleza didáctica: no impone una única forma de multiplicar, sino que ofrece otra vía para comprender lo mismo.
Cómo aplicar la celosía paso a paso con un ejemplo
Antes de lanzarte a ejercicios largos, conviene practicar con números modestos para afianzar la mecánica. A continuación, verás un ejemplo tipo, con pautas generales que puedes replicar con cualquier par de números. Aunque aquí lo expliquemos por escrito, recuerda que, al montar tu cuadrícula, cada casilla se parte por una diagonal y en ella colocas el producto de dos dígitos: decena arriba, unidad abajo. De este modo, el tablero se llena de microresultados que luego se agregan.
Supongamos que quieres multiplicar 347 por 26. El primer número tiene tres cifras y el segundo, dos; por tanto, dibuja una cuadrícula de 3 columnas por 2 filas, con diagonales que bajen de izquierda a derecha. Coloca 3, 4 y 7 en la parte superior, alineados sobre las columnas, y 2 y 6 a la izquierda de las filas. Ahora, en cada casilla, multiplica el dígito de la columna por el de la fila. Si el resultado es de una cifra, sitúalo en la parte de unidades; deja la decena como 0 arriba. Si es de dos cifras, reparte: decena arriba de la diagonal y unidad abajo. Llena así todas las casillas.
Al terminar, realiza la suma por diagonales empezando por la esquina inferior derecha. Cada diagonal te da una cifra del resultado; si superas 9, llevas las decenas a la diagonal siguiente, exactamente igual que en la suma tradicional. Cuando completas todas las diagonales, vas leyendo el número de derecha a izquierda (o de la última diagonal a la primera), formando el resultado final. Este barrido diagonal es lo que hace tan ordenado el proceso: nunca mezclas lugares de unidades, decenas o centenas.
Para consolidar, repite con multiplicaciones de dos cifras por dos cifras. Observa patrones: al intercambiar el orden de los factores (conmutativa), la cuadrícula queda simétrica; esto es un refuerzo visual de propiedades que ya conoces. Y, si te animas con números más largos, simplemente añade columnas o filas según sea necesario. El método escala bien porque crece la rejilla pero no aumenta la dificultad conceptual.
Algunas sugerencias para la práctica: usa lápices de colores distintos para rellenar decenas y unidades, o para destacar cada diagonal de suma; marca con un pequeño punto las diagonales donde has hecho una llevada, para no perder el hilo; y, cuando lo trabajes en grupo, alterna quién multiplica y quién suma, promoviendo que cada estudiante asuma un rol y verbalice lo que está haciendo.
Ventajas, errores frecuentes y soluciones prácticas
Entre sus ventajas, destaca la reducción del estrés por “filas y columnas” del algoritmo tradicional y la claridad de cada producto parcial. Muchas personas aprenden mejor si ven cada paso separado y, al mismo tiempo, conectado a la estructura del número final. Esa visibilidad hace que los errores se detecten antes: si una casilla no cuadra, la diagonal revelará la incoherencia durante la suma.
- Ventaja visual: la diagonal separa automáticamente decenas y unidades en cada producto parcial.
- Organización: cada casilla tiene un sentido único, evitando desplazar cifras por error.
- Escalabilidad: funciona igual de bien con dos cifras que con cinco, ampliando la rejilla.
- Refuerzo conceptual: enlaza la multiplicación con el valor posicional y la suma final.
Errores típicos a vigilar: escribir las dos cifras del producto parcial en la misma mitad de la casilla; olvidar completar casillas periféricas; y, el más común, confundir la dirección de las diagonales al sumar. Para todos ellos, ayuda seguir una rutina constante: primero completa fila por fila; luego revisa que cada casilla tenga decena arriba y unidad abajo; finalmente, suma diagonales de derecha a izquierda, anotando llevadas. Con esta disciplina, los fallos se reducen de forma notable en pocas sesiones.
Otro problema habitual es la gestión de llevadas en diagonales cuando aparecen sumas largas (por ejemplo, al multiplicar números con muchas cifras). Solución: anota pequeñas marcas junto a la diagonal donde se genera la llevada y, en la siguiente, añade esa decena al inicio de la suma. Alternativamente, puedes escribir la llevada en la parte superior entre dos diagonales, como recordatorio. Lo importante es no mezclar llevadas con productos parciales ya escritos: mantenlas siempre fuera de las casillas.
Si trabajas con niñas y niños que aún confunden el valor posicional, adopta apoyos visuales extra: colorea en un tono suave las regiones de unidades y decenas de cada diagonal, o imprime plantillas con diagonales más gruesas. También funciona repartir tarjetas con cifras del 0 al 9 para montar la rejilla manipulativamente antes de pasar al cuaderno. Estas estrategias convierten la celosía en una experiencia tangible y memorable.
Finalmente, al combinar la celosía con el método tradicional, anima a comparar resultados para comprobar consistencia. Cuando se detecte una discrepancia, el tablero sirve como mapa para rastrear el paso donde hubo confusión. A medio plazo, muchas personas ganan confianza y dominan ambos enfoques, eligiendo según el contexto. Esa autonomía es, al fin y al cabo, una meta central del aprendizaje matemático significativo.
Aplicaciones y progresión: de 3.º a 5.º y más allá
En 3.º y 4.º de Primaria, la celosía se puede introducir con dos cifras por una cifra, saltando después a dos por dos. Es clave no precipitarse: cada casilla es una oportunidad para practicar tablas de multiplicar en contexto. En 5.º, ya es razonable abordar multiplicaciones de tres por dos o tres por tres cifras. En estas edades, el método se convierte en un aliado para saltar del cálculo mecánico a la reflexión sobre el valor posicional. Esta progresión ayuda a que, cuando llegue la multiplicación por números grandes, el alumnado sienta que todo es “más de lo mismo”, solo con una rejilla mayor.
También resulta útil para alumnado con diferentes ritmos. Quien va más rápido puede encargarse de completar más casillas o de verificar diagonales, mientras que quien necesita más tiempo puede centrarse en productos parciales. De esta manera, se integran las diferencias en una misma actividad compartida y se fomenta la colaboración. Con un banco de plantillas listas para imprimir, la preparación de la clase se simplifica sin perder calidad.
Un apunte para familias: practicar en casa no requiere materiales especiales. Basta papel cuadriculado o una hoja en blanco y una regla. Si se desea, se puede plastificar una plantilla para escribir con rotulador borrable y reutilizarla. En sesiones de 10-15 minutos, dos o tres veces por semana, la mejora suele ser notable porque el método da feedback visual inmediato y permite corregir sobre la marcha.
En cursos posteriores, la celosía es un buen punto de partida para hablar de multiplicaciones polinomiales, ya que existe un paralelismo entre “productos parciales por casilla” y “términos por término”. Sin forzar contenidos, se puede mostrar que la organización del tablero refleja cómo se combinan componentes de mayor orden. Esta conexión conceptual, para quienes sienten curiosidad, ensancha la utilidad más allá del cálculo aritmético básico.
Recursos en español y apoyos para un aprendizaje efectivo
Además de esta guía detallada, merece la pena contar con materiales de consulta rápida. Existe un PDF en español, pensado para cursos de 3.º a 5.º, que condensa el método en tres páginas con ejemplos visuales. Es un documento breve, alojado en una biblioteca pública, que ha recibido en torno a 946 visualizaciones y que resulta ideal como hoja de habilidades o recordatorio para casa y aula. Puedes consultarlo y descargarlo desde aquí: PDF del método de multiplicación de celosía (español). Este tipo de recurso, al ser conciso y claro, complementa perfectamente una explicación más extensa como la que acabas de leer.
En paralelo, es útil reflexionar sobre el entorno de aprendizaje. Muchas familias observan que, pese a horas y horas de clase, los resultados no siempre llegan. Cuando esto ocurre, no se trata de “echarle más tiempo” sin dirección, sino de mejorar cómo se aprende. Hay propuestas educativas que combinan tecnología actual y un enfoque integral del proceso, con la idea de asegurar que cada estudiante avance de verdad. Bajo esta filosofía, se plantea que, si algo no está funcionando, hay que ajustar la metodología y el seguimiento hasta que funcione.
Un enfoque de este tipo suele apoyarse en herramientas de diagnóstico, práctica adaptativa y acompañamiento cercano. La idea es garantizar que los contenidos se dominen y que el estudiante disponga de más oportunidades de éxito. Cuando se aplica a matemáticas, esto significa diseñar actividades que integren métodos como la celosía, recursos visuales y evaluación continua, de manera que quienes se atascaban con el algoritmo tradicional puedan experimentar una mejora progresiva. En definitiva, lo importante es transformar el tiempo de estudio en aprendizaje efectivo.
Si te reconoces en el escenario de “mucho esfuerzo pero pocos resultados”, considera combinar guías prácticas como este artículo, un PDF de apoyo y, si es necesario, un plan de trabajo más amplio que abarque motivación, hábitos, tecnología y refuerzo personalizado. Cuando la intervención se hace de forma integral (lo que a veces se denomina una metodología 360°), la curva de aprendizaje se acelera con menos frustración. Para las familias, esta visión se parece más a una “garantía de aprendizaje” que a una apuesta a ciegas: no basta con estar horas; hay que medir, orientar y acompañar.
Ya tienes un mapa completo: qué es el método de la celosía, cómo se construye su rejilla paso a paso, por qué encaja tan bien en 3.º-5.º de Primaria, qué ventajas aporta frente a errores comunes y qué recursos en español puedes consultar, incluyendo un PDF de tres páginas muy difundido. Al integrar apoyos visuales, rutina de práctica y, si procede, una estrategia educativa más amplia, la multiplicación deja de ser un muro y se convierte en una secuencia de pasos claros; es ahí donde la celosía brilla, porque convierte la complejidad en orden y la incertidumbre en procedimientos confiables.